ÖZEL GEBZE ARTI AKŞAM LİSESİ
-
Hangi sayılar hem pozitif hem de tam sayılardır?
A) Doğal Sayılar
B) Rasyonel Sayılar
C) İrrasyonel Sayılar
D) Tamsayılar
E) Gerçek Sayılar
-
4(x - 3) - 3(x + 1) = 9 denkleminin çözümü nedir?
A) -2 B) 0 C) 2 D) 4 E) 24
-
3x - 4 = 7x - 8 denklemi için x'in değeri nedir?
A) 2 B) 3 C) 4 D) 5 E) 6
-
4x + 5 = 3x - 2 denklemi için x'in değeri nedir?
A) -7 B) -1 C) 1 D) 7 E) 13
-
|2x - 1| = 5 denklemi için x'in alabileceği değerler kümesi nedir?
A) {-2, 3} B) {3/2, -2} C) {3/2, 1/2} D) {-3, 2} E) {3, -1}
-
3x + 2y = 8 ve x - y = 3 denklemleri için (x,y) çifti nedir?
A) (4, 1) B) (5, 2) C) (6, 3) D) (7, 4) E) (8, 5)
-
2^(2x+1) - 2^(x+1) - 6 = 0 denkleminin çözüm kümesi nedir?
A) {-2, 1} B) {-1, 2} C) {0, 3} D) {1, 4} E) {2, 5}
-
3^(x-1) + 3^(-x+1) = 10 denkleminin çözüm kümesi nedir?
A) {0, 2} B) {1, 3} C) {-1, 1} D) {-2, 0} E) {-3, -1}
-
120 sayısının bölenlerinden kaç tanesi 3'e ve 5'e birden bölünebilir?
A) 2 B) 3 C) 4 D) 5 E) 6
-
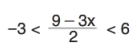
eşitsizliğinin çözüm kümesinde kaç tane tam sayı olduğunu bulunuz.
-
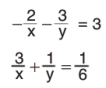
olduğuna göre x'i bulunuz.
-
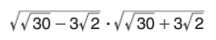
işleminin sonucunu bulunuz.
-
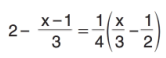
denkleminin kökünü bulunuz.
-
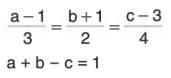
olduğuna göre b'nin değerini bulunuz.
-
(5x - 3)4 = (4x - 6)4 olduğuna göre X'in alabileceği değerleri bulunuz.
-
x ve y birer gerçek sayıdır.
-3 < x < 1
3 < y < 4
olduğuna göre 2x-7 ifadesinin alabileceği en büyük tam sayı değeri ile en küçük tam sayı değerinin toplamını bulunuz.
ÖZEL GEBZE ARTI AKŞAM LİSESİ CEVAPLARI
-
Hangi sayılar hem pozitif hem de tam sayılardır?
A) Doğal Sayılar
B) Rasyonel Sayılar
C) İrrasyonel Sayılar
D) Tamsayılar
E) Gerçek Sayılar -
4(x - 3) - 3(x + 1) = 9 denkleminin çözümü nedir?
A) -2 B) 0 C) 2 D) 4 E) 24
-
3x - 4 = 7x - 8 denklemi için x'in değeri nedir?
A) 2 B) 3 C) 4 D) 5 E) 6
-
4x + 5 = 3x - 2 denklemi için x'in değeri nedir?
A) -7 B) -1 C) 1 D) 7 E) 13
-
|2x - 1| = 5 denklemi için x'in alabileceği değerler kümesi nedir?
A) {-2, 3} B) {3/2, -2} C) {3/2, 1/2} D) {-3, 2} E) {3, -1}
-
3x + 2y = 8 ve x - y = 3 denklemleri için (x,y) çifti nedir?
A) (4, 1) B) (5, 2) C) (6, 3) D) (7, 4) E) (8, 5)
-
2^(2x+1) - 2^(x+1) - 6 = 0 denkleminin çözüm kümesi nedir?
A) {-2, 1} B) {-1, 2} C) {0, 3} D) {1, 4} E) {2, 5}
-
3^(x-1) + 3^(-x+1) = 10 denkleminin çözüm kümesi nedir?
A) {0, 2} B) {1, 3} C) {-1, 1} D) {-2, 0} E) {-3, -1}
-
120 sayısının bölenlerinden kaç tanesi 3'e ve 5'e birden bölünebilir?
A) 2 B) 3 C) 4 D) 5 E) 6
-
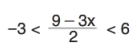
eşitsizliğinin çözüm kümesinde kaç tane tam sayı olduğunu bulunuz. -
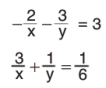
olduğuna göre x'i bulunuz. -
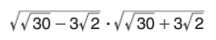
işleminin sonucunu bulunuz. -
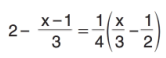
denkleminin kökünü bulunuz. -
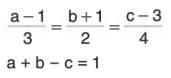
olduğuna göre b'nin değerini bulunuz. -
(5x - 3)4 = (4x - 6)4 olduğuna göre X'in alabileceği değerleri bulunuz.
-
x ve y birer gerçek sayıdır.
-3 < x < 1
3 < y < 4
olduğuna göre 2x-7 ifadesinin alabileceği en büyük tam sayı değeri ile en küçük tam sayı değerinin toplamını bulunuz.
Bu sorunun cevap anahtarı D) Tamsayılar olarak verilmiştir. Pozitif sayılar, sıfırdan büyük olan sayılardır. Tam sayılar ise pozitif sayıları, sıfırı ve negatif sayıları içerir. Dolayısıyla, pozitif tam sayılar hem pozitif hem de tam sayılardır. Doğal sayılar yalnızca pozitif tamsayıları içerirken, rasyonel sayılar kesirli sayıları ve ondalık gösterimi sonlu veya sonsuz olan sayıları içerir. İrrasyonel sayılar ise ondalık gösterimi sonsuz olan ancak kesirli bir oranı olmayan sayılardır. Gerçek sayılar ise tüm rasyonel ve irrasyonel sayıları içerir.
Bu denklemi çözmek için öncelikle parantezleri açmalı ve benzer terimleri bir araya getirmeliyiz. Böylece:4(x-3) - 3(x+1) = 9. 4x - 12 - 3x - 3 = 9. x - 15 = 9. x = 24. Cevap anahtarı: E
Bu denklemi çözmek için x'i bir tarafta toplamalı ve sabitleri diğer tarafa taşımalısınız. Öncelikle, 3x - 4 = 7x - 8 denklemindeki x'i bir tarafa toplamak için, her iki tarafı da 3x ile çarpabilirsiniz. Bu, 3x - 4 = 7x - 8 denklemini 3x - 4 = 7x - 8 olarak yeniden yazacaktır. Daha sonra, sabitleri diğer tarafa taşımak için, her iki tarafı da 4 ile toplayabilirsiniz. Bu, 3x = 7x - 4 olarak yeniden yazacaktır. Son olarak, her iki tarafı da 7x'in katsayısı olan 3 ile bölebilirsiniz. Bu, x = 2 olarak çözümü verir. Cevap Anahtarı: A) 2. Verilen denklemde, x'in değerini bulmak için x'i bir tarafa toplayıp sabitleri diğer tarafa taşıdık. Bu işlem sonucunda x = 2 olarak çözümü bulduk.
Bu denklemde 4x ve 3x terimleri x'in katsayısıdır ve 5 ve -2 terimleri sabittir. Denklemi çözmek için, ilk olarak her iki tarafın da aynı değeri koruması için 3x terimini sol tarafa getirmeliyiz. Böylece, 4x - 3x = -2 - 5 şeklinde bir denklem elde ederiz. Basitçe çözerek, x = -7 olduğunu buluruz.
Cevap anahtarı B'dir, yani {3/2, -2}. İki olası durum vardır: 2x - 1 = 5 veya 2x - 1 = -5. İlk durumda, 2x = 6 olduğundan x = 3 olur. İkinci durumda ise 2x = -4 olduğundan x = -2 olur. Bu nedenle, |2x - 1| = 5 denklemi için x'in alabileceği değerler kümesi {3/2, -2}'dir.
Bu soru iki lineer denklemle ilgilidir. İlk denklemde 3x+2y=8, ikinci denkleme x-y=3 denir. İkinci denklemin çözümü y=x-3 olarak elde edilir. Bu eşitliği, 3x+2y=8 denkleminin sol tarafına yerleştirdiğimizde 3x+2 (x-3) = 8 olarak yazabiliriz. Bu eşitliği çözerek, x=4'i buluruz. Bu değeri, y=x-3 eşitliğine yerleştirerek, y=1 elde ederiz. Dolayısıyla, (x,y) çifti (4,1) olarak bulunur.
Bu denklemi çözmek için, öncelikle her iki tarafı da 2^(x+1) ile bölebiliriz. Böylece elde edeceğimiz denklem 2^(x+1) * (2^(x) - 1) - 6 = 0 olacaktır. Sonra, 2^(x) = y şeklinde bir değişken dönüşümü yaparak y^2 - y - 6 = 0 denklemini elde ederiz. Bu denklemin çözüm kümesi yani y değerleri {-2, 3} olur. Yerine x = log2(y) değerlerini yerleştirerek, x = -2 veya x = 1 elde ederiz. Bu nedenle doğru cevap A seçeneğidir.
Verilen denklemin çözüm kümesi {1,3}'tür. Çözüm açıklaması: Denklem, x'in pozitif ve negatif tüm reel değerleri için çözülebilir. Ancak, denklemdeki terimlerin birbirine eşit olduğunu fark edersek, x'i bulabiliriz. İlk olarak, her iki tarafı 3^(x-1) ile çarpalım ve denklemi şu şekilde yeniden yazalım: 3^(2x-2) + 1 = 10 * 3^(x-1) Şimdi, bu denklemi bir ikinci dereceden denklem haline getirmek için 3^(x-1)'i t'yı kabul edelim:t^2 - 10t + 1 = 0 Bu denklem, t=1 ve t=9 olmak üzere iki gerçek köke sahiptir. Buradan t=3^(x-1) olduğundan, x'i bulmak için 3^(x-1) = 1 ve 3^(x-1) = 9 durumlarına bakalım. İlk durumdan, x-1=0 olduğu için x=1, ikinci durumdan, x-1=2 olduğu için x=3 sonucunu elde ederiz.
Soru, 120 sayısının hem 3'e hem de 5'e bölünebilen bölenlerinin sayısını istemektedir. 120 sayısı, 3 ve 5'in çarpımına eşit olduğundan, sadece 3 ve 5'in çarpımı olan 15 ve 120 sayıları bu kritere uygun bölenlerdir. Ayrıca, herhangi bir sayının bölenleri, kendisi hariç en fazla yarısına kadar olan pozitif tam sayılardan oluşur. 120 sayısının yarısı 60 olduğundan, 120 sayısının en fazla 60 böleni vardır. Dolayısıyla, 3'e ve 5'e birden bölünebilen bölenlerin sayısı en fazla 2 olabilir. Cevap A şıkkıdır.
.
Açıklama:.
Açıklama:.
Açıklama:.
Açıklama:.
Açıklama:.
Açıklama:.
Açıklama:Yorum Bırak
ÖZEL GEBZE ARTI AKŞAM LİSESİ Detayları
ÖZEL GEBZE ARTI AKŞAM LİSESİ 1 kere indirildi. Bu sınav Orta derecede zorluktadır. Sınav zorluk derecesi sınavı oluşturan soruların istatistikleri alınarak oluşturulmuştur. Toplamda 16 sorudan oluşmaktadır. Sınav soruları aşağıda verilen kazanımları ölçecek şekilde hazırlanmıştır. 13 Ekim 2024 tarihinde eklenmiştir. Bu sınavı şimdiye kadar 0 kullanıcı beğenmiş. ÖZEL GEBZE ARTI AKŞAM LİSESİ yazılı sınavına henüz hiç yorum yapılmamış. İlk yorum yapan siz olun.ÖZEL GEBZE ARTI AKŞAM LİSESİ sınavında hangi soru türleri kullanılmıştır?
Bu sınavda verilen soru türleri kullanılmıştır.- Test
- Klasik
ÖZEL GEBZE ARTI AKŞAM LİSESİ Hangi Kazanımları Kapsıyor?
Bu sınav ve tema ve kazanımlarını kapsamaktadır.- BÖLÜNEBİLME
- Bölünebilme Kuralları
Ayrıca üslü SAYILAR
Pozitif tam sayıları tanımlama ve sınıflandırma becerisi.
Basit matematiksel denklemleri çözebilme.
Verilen denklemleri çözebilme yeteneği.
Denklem çözme becerisini ve matematiksel düşünme yeteneğini ölçer.
Matematikteki mutlak değer kavramını anlama ve mutlak değer denklemlerini çözme becerisi.
lineer denklem çözme becerilerini ölçmektedir.
Üst ve logaritma fonksiyonları ile ilgili denklem çözme becerisidir.
Verilen denklem, matematiksel işlemler kullanarak çözülebilir. Denklemin her iki tarafındaki terimleri eşitlersek, bir ikinci dereceden denklem elde ederiz. Bu denklemin çözümleri, orijinal denklemin çözüm kümesini belirler.
Verilen bir sayının bölenlerinin sayısını hesaplayabilme.
etiketlerini kapsamaktadır.Hangi kategoriye ait?
ÖZEL GEBZE ARTI AKŞAM LİSESİ sınavı 9.Sınıf kategorisinin Matematik alt kategorisinin, 2 dönemine ait.ÖZEL GEBZE ARTI AKŞAM LİSESİ Sınavını hangi formatta indirebilirim?
ÖZEL GEBZE ARTI AKŞAM LİSESİ sınavını .pdf veya .docx olarak ücretsiz indirebilirsiniz. Bunun yanında sistem üzerinden doğrudan yazdırabilirsiniz. Veya öğretmen olarak giriş yaptıysanız ÖZEL GEBZE ARTI AKŞAM LİSESİ sınavını sayfanıza kaydedebilirsiniz.ÖZEL GEBZE ARTI AKŞAM LİSESİ sınav sorularının cevap anahtarlarını nasıl görebilirim?
Sınavın cevap anahtarını görebilmek için yukarıda verilen linke tıklamanız yeterli. Her sorunun cevabı sorunun altında gösterilecektir. Veya Sınavı .docx olarak indirdiğinizde office word programıyla açtığınızda en son sayfada soruların cevap anahtarına ulaşabilirsiniz.Kendi Sınavını Oluştur
Değerli öğretmenlerimiz, isterseniz sistemimizde kayıtlı binlerce sorudan 9.Sınıf Matematik dersi için sınav-yazılı hazırlama robotu ile ücretsiz olarak beş dakika içerisinde istediğiniz soru sayısında, soru tipinde ve zorluk derecesinde sınav oluşturabilirsiniz. Yazılı robotu için Sınav Robotu tıklayın.
Sınav hakkında telif veya dönüt vermek için lütfen bizimle iletişime geçin.